What is Elliptic Curve Cryptography?
To explore Elliptic Curve Cryptography, we must first discuss public-key cryptography (PKC) schemes.
All PKC schemes have in common that they are based on key pairs - a public and a private key. This is also referred to as asymmetric cryptography.
While a public key can be distributed openly to any potential sender of an encrypted message, only the owner of the corresponding private key can decrypt those messages. The public key is generated from the private key using a mathematical one-way function.
PKC schemes can also be used to create digital signatures.
Digital signatures are created using a message to be signed and a private key as an input. A verifier can validate the signature using the corresponding public key without gaining knowledge about the private key used to sign the message.
Public-Key Cryptography
Public-key cryptography is mostly used for the confidential exchange of information like encrypted emails using Pretty Good Privacy (PGP) or similar encryption methods. Other use cases are sender authentication using digital signatures and verifying ownership in cryptocurrencies.
One can also construct hybrid cryptosystems composed of symmetric and asymmetric cryptographic schemes.
Asymmetric cryptography is computationally more expensive than symmetric schemes.
In hybrid cryptosystems, a PKC scheme is used to initialize a secure communication by exchanging a key for asymmetric encryption first. After that, the participants use the symmetric scheme to reduce computational overhead.
Especially when large amounts of data need to be securely transmitted this type of hybrid system is useful.
Two of the most popular PKC schemes are:
- ECC: Elliptic Curve Cryptography
- RSA: Rivest - Shamir - Adleman
ECC - Elliptic Curve Cryptography
Elliptic curve cryptography is based on discrete mathematics. In discrete math, elements can only take on certain discrete values.
Boolean algebra is an example of discrete math where:
- The possible values are zero and one
- These values are usually interpreted as true and false
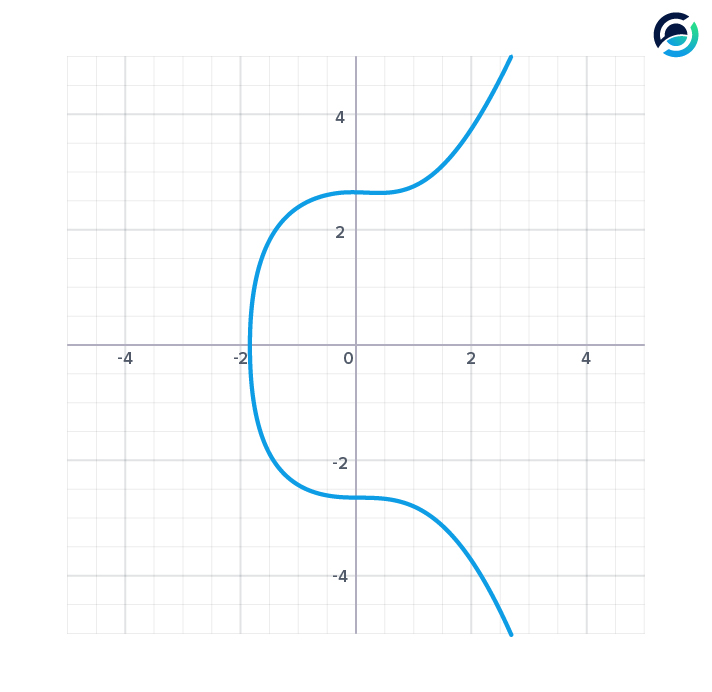
Math on the elliptic curve uses familiar mathematical operations such as addition and subtraction, but the effect of these operations is defined by the curve.
Instead of having a set of rational or whole numbers as possible values, the allowed discrete values are defined by the curve. Any point on the curve is a possible value.
Each number is in the set of points that make up the curve. A point on the curve can be interpreted as a vector.
Vectors and Scalars
Vectors represent quantities that have both, a direction and a magnitude.
The double describing the two-dimensional vector in the graphic below can be one of two things: either a pair of x and y-coordinates, or an angle , enclosed between the arrow and x-axis, and the length of the arrow.
On the elliptic curve, any point can be viewed as an arrow pointing in a certain direction and having a defined magnitude or length (also called a vector).
A scalar is a single value, like an integer that only has a magnitude but no direction.

Multiplication and division are also defined on the curve. The multiplication of a point on the curve with a scalar is easy to perform, the division of a point is computationally difficult.
It is crucial for any PKC scheme to be able to easily compute a public key from a private key but the reverse operation must be infeasible. Being able to easily perform multiplications on a curve but unable to perform division efficiently creates the basic building block of a PKC scheme.
The infeasibility of performing division on the elliptic curve is called the discrete logarithm problem or sometimes also called the elliptic curve discrete logarithm problem (ECDLP).
While all this might sound very complex at first you will see shortly that a graphical approach is sufficient to develop an intuition for the math used on elliptic curves.
Math on the Elliptic Curve
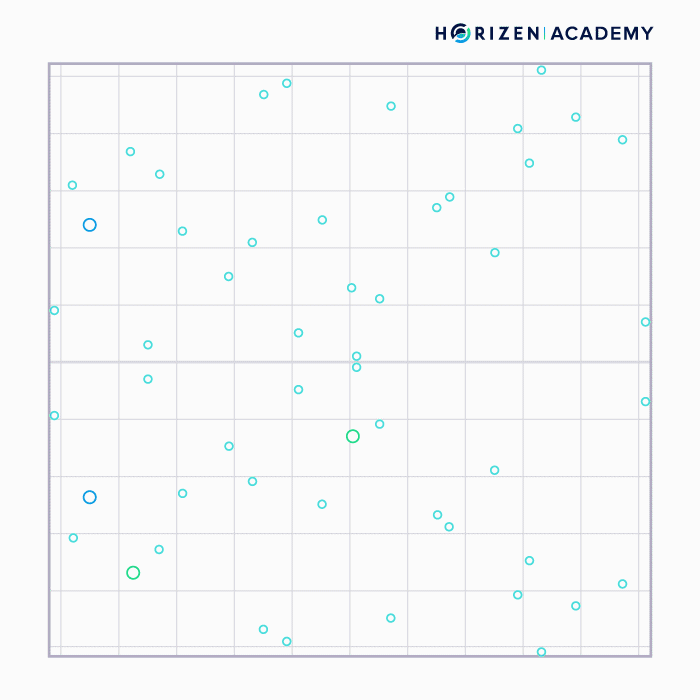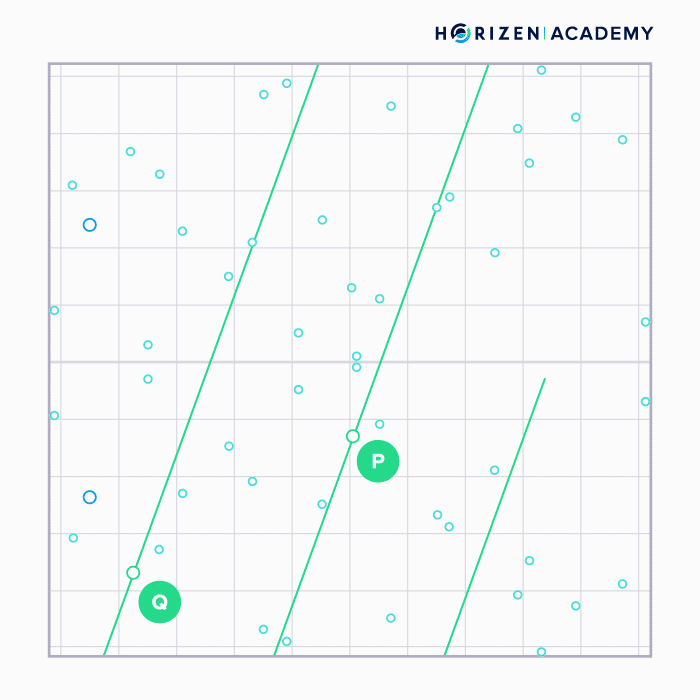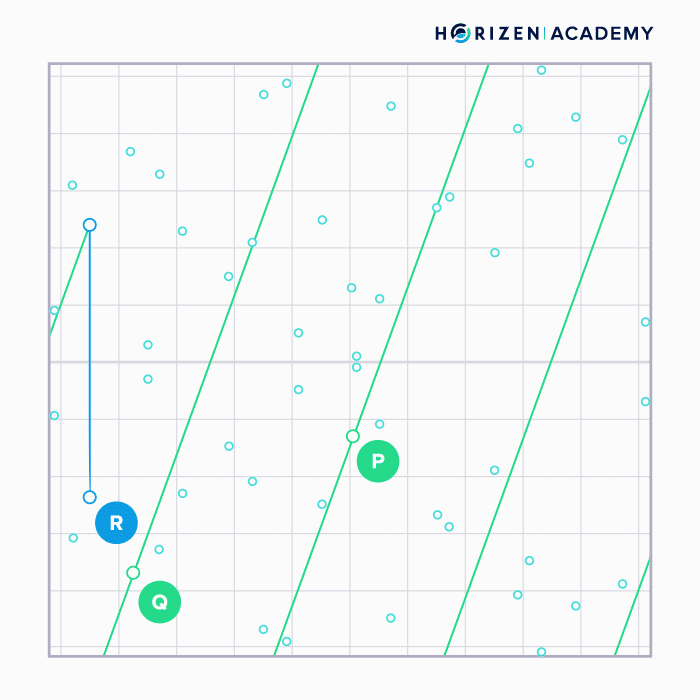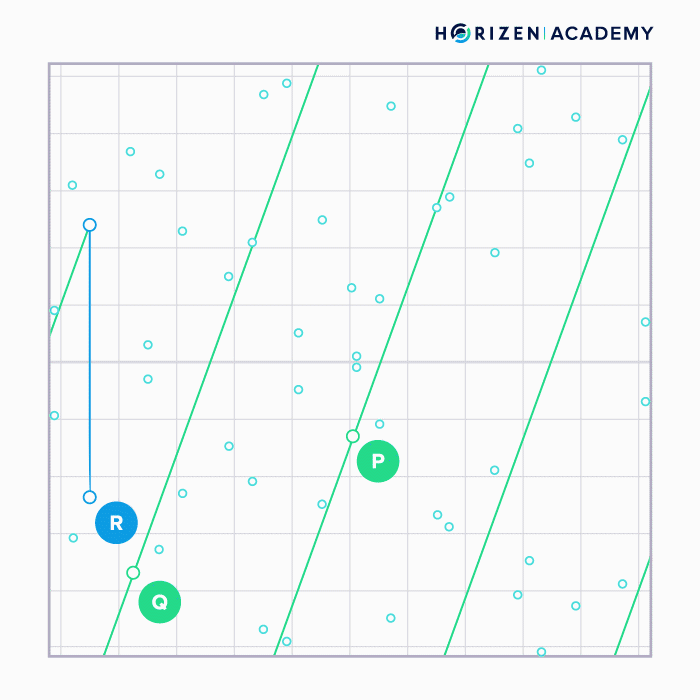
Adding two points (P and Q) on the curve can be done graphically by connecting them with a straight line, taking the intersection of that line with the curve and projecting it across the x-axis (R).
When a point is added to itself the tangent line at that point is taken, the intersection with the curve found and again projected across the x-axis.
Note how the graphical approach does not allow you to perform division. You would start by projecting the point R back across the x-axis, but finding the straight line that yielded the intersection you are looking for is infeasible.
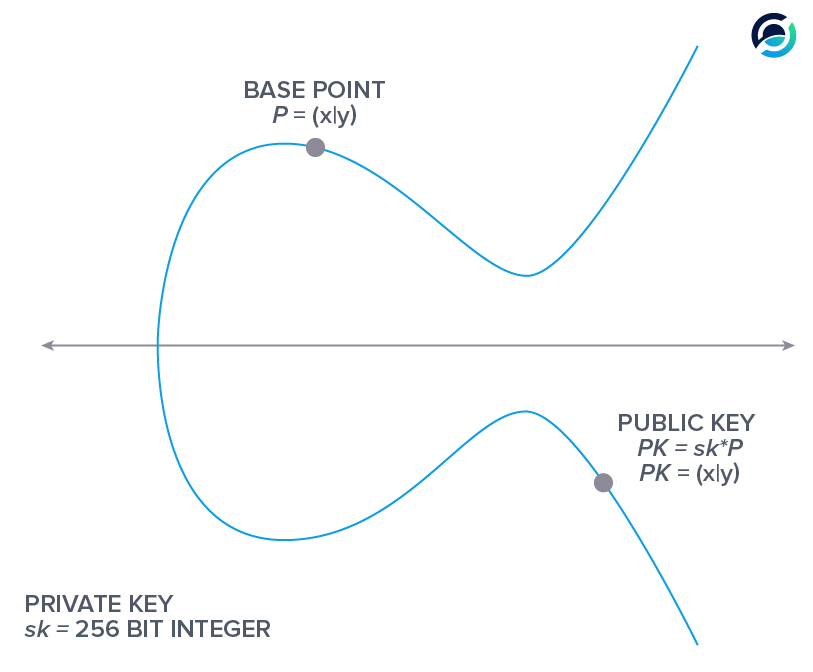
Your private key is a large random number, which when multiplied with a base point, sometimes also called generator point, on the curve yields your public key.
The key takeaway is that your private key is a large random number or scalar, which multiplied with the base point yields your public key, another point on the curve that can also be referred to as a vector.
The elliptic curve is generally described by where .
There are two possible solutions for each x-value, which is very useful when compressing a point on the curve, like the base point or your public key. One can omit the y-coordinate and include an extra bit indicating if the y-value is positive or negative without losing any information.
In Bitcoin and Horizen, the curve used is called secp256k1 and described by .
The base points coordinates are:
and
Multiplying Large Numbers on the Curve
How hard does your computer have to work in order to perform multiplication on the curve with large numbers like your private key and the base point ?
Let's use a simple example first and look at how many steps it takes to get the product .
The first thing that might come to mind is performing 9 point additions:
Because the distributive property...
...holds for math on the elliptic curve, one can reduce the number of steps to calculate to four:
To compute , where x is a random 256-bit integer, read: your private key, it never takes more than 510 point operations.
That is although x can be huge! It can range between 0 and which can be written out as:
In a first step you will use the property:
You can calculate the series below with just 255 point addition operations. You keep adding P to itself in order to expand the series by one element:
Now that we have calculated and saved the series above, we need to find the binary expansion of x. If x was 222, the binary expansion would be:
Then the binary expansion is multiplied by P.
The individual points don't need to be calculated because we have already completed this step. The maximum size of our expansion includes 256 elements .
Adding them together means performing 255 point additions. So how much work has our computer done so far?
We have calculated the series...
...with 255 computational steps and computed our desired with a maximum of 255 additional steps, totalling 510 point addition operations at maximum.
Because of the discrete log problem the computation we just performed is not reversible, there is no known algorithm for it.
Let's give all of this some context again.
Your private key is a random 256-bit integer. This means it will be somewhere between 0 and .
In order to determine a private key from a public key you would have to perform point addition operations on average because guessing or applying brute force is the most efficient way known.
If your computer could perform a trillion, additions per second and you had been running your computer since the beginning of the universe, you would only have computed point additions by now which equals just about 0.00000009% of the total work to derive a single private key from a public key - on average.
Elliptic curve cryptography is a good basis for a public-key cryptography scheme. It is infeasible to derive a public key from a private key.
The Finite Field
In order to avoid points that can't be stored in a 512-bit integer, read: an uncompressed public key, the curve is defined over a finite field that only allows coordinates up to a certain size. We transform...
to
...where p is a large prime.
For the secp256k1 curve used in Bitcoin and Horizen, p is the largest prime that is less than .
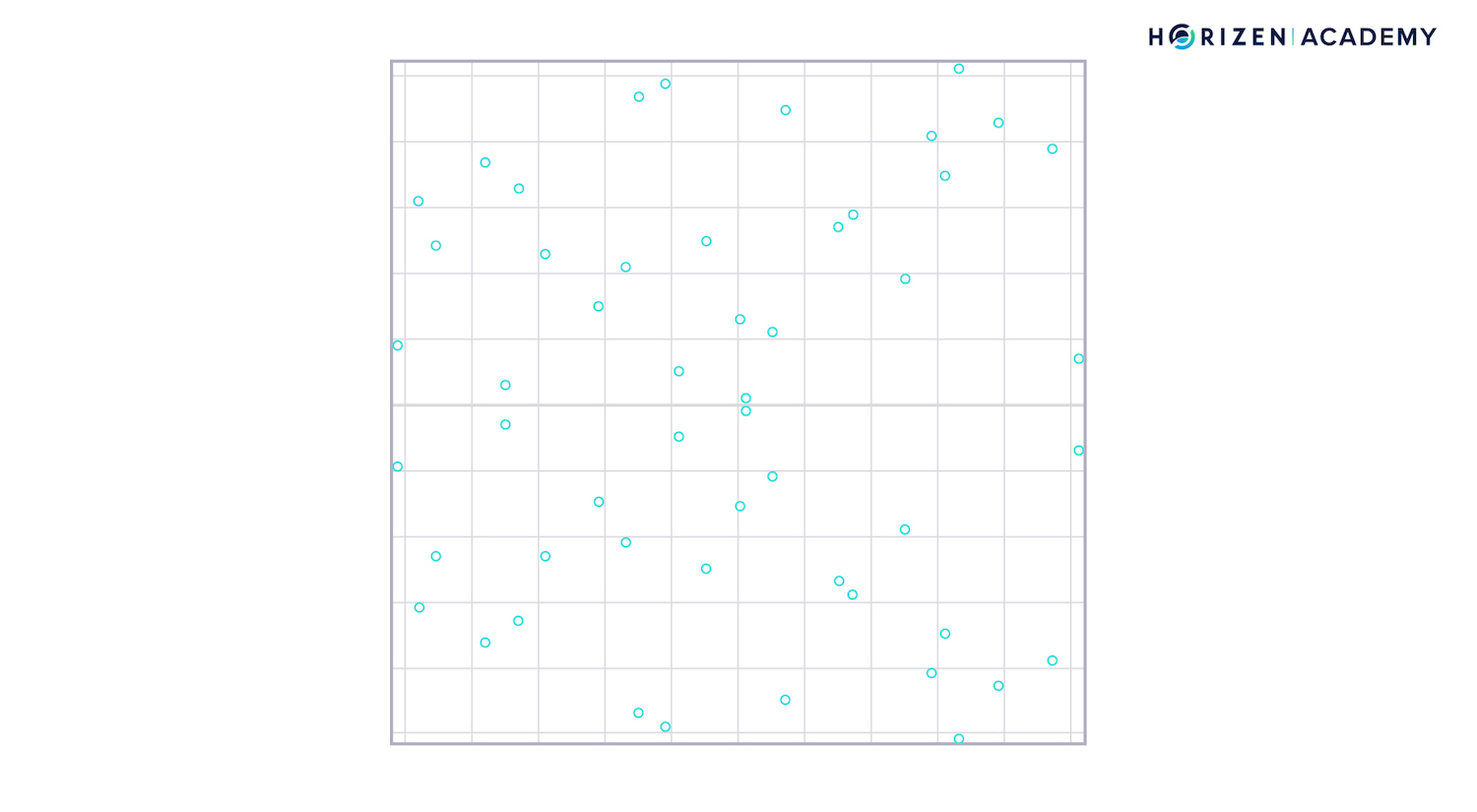
The graph above shows the finite field where each point represents a valid, discrete value of a point on the curve. Notice how the symmetry with regards to the x-axis is preserved.
In order to graphically add two points together, one again connects them with a straight line. This line may "wrap around" the field several times before it intersects with another point or discrete value: the result of the addition R.
Please note that in reality, the finite field is multidimensional. The two-dimensional finite field shown here only serves as an easy to follow example.
RSA - Rivest, Shamir, Adleman
Before ECC became popular, almost all public-key schemes were built using cryptosystems based on modular arithmetic, such as RSA (Rivest - Shamir - Adleman).
The security of all PKC schemes is based on one main assumption:
It must be infeasible to derive a private key from the corresponding public key.
As we said before, public keys are derived from a private key using a mathematical one-way function. The security is therefore based on the computational hardness of reversing the one-way function.
With PKC schemes like RSA, using modular arithmetic, the security is based on the assumed hardness of integer factorization. "Assumed" because there is no known way of proving unconditional hardness.
In elliptic curve cryptography, the security assumption is based on the hardness of the discrete log problem.
RSA and its modular-arithmetic-based friends are still important today and are often used alongside ECC. Rough implementations of the mathematics behind RSA can be built and explained rather easily.
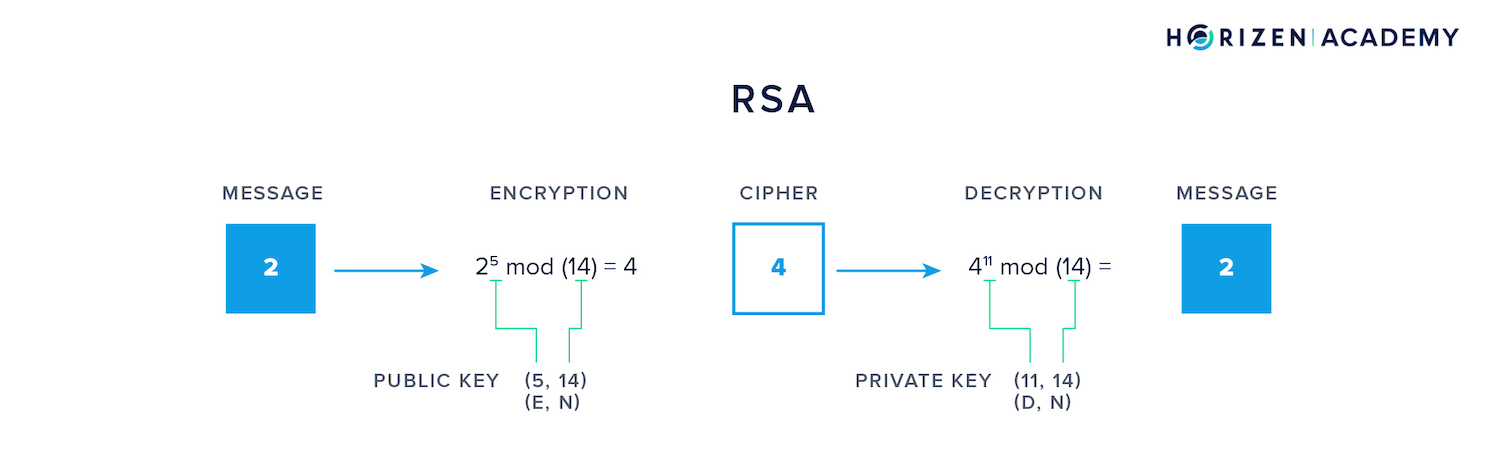
Above is a rudimentary example of encrypting a message (2) with a public key that comprises a tuple of two values: the encryptor E and the modulus N.
The cipher (4) is later decrypted using the corresponding private key comprising the tuple decryptor D and the same modulus N. The interesting part is the relation between the three value E, D and N.
To keep this article at a reasonable length, we refer the interested reader to this very understandable RSA article for an explanation of how these values are related. A simple RSA implementation accompanied by python code can be found here.
Summary - Elliptic Curve Cryptography
Public-key cryptography is used in secure communication and sender authentication using digital signatures. Proving ownership in cryptocurrencies is a special case of sender authentication.
The security of a given PKC scheme hinges on the assumption that the one-way function used to derive a public key from a private key is computationally difficult to reverse.
ECC is based on discrete math where only certain values are allowed. The security is based on the hardness of the discrete logarithm problem.
RSA and many of the early PKC schemes are built using modular arithmetic and the security is based on the hardness of integer factorization.
When you are transferring cryptocurrencies you generally use addresses and not your public key.
Cobalt is a secure and easy-to-use web extension wallet for the Horizen cross-chain ecosystem. Trustworthy, reliable and built to easily manage your assets.