What is a Wallet Address?
When you install and set up a wallet on your phone or computer, the first thing you will do is actually fund your wallet by transferring some crypto to your address.
Lets take a look at where wallet addresses come from and how they relate to private keys.
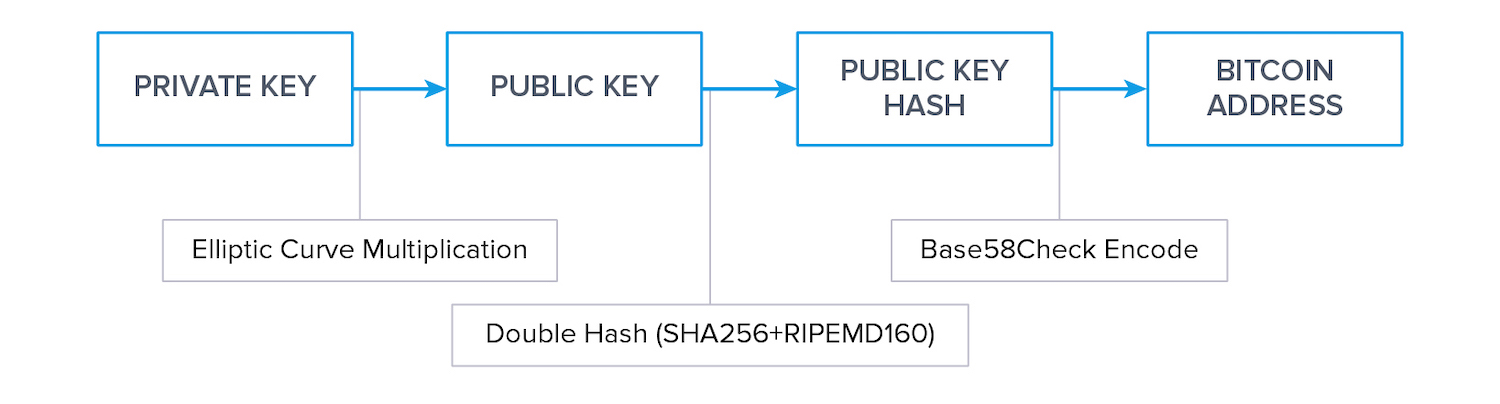
How are Wallet Addresses Derived?
First, a private key is randomly generated. Then, a public key is derived from the newly generated private key through elliptic curve multiplication.
Wallet addresses are derived from public keys in two main steps:
- By hashing the public key
- By Base58Check encoding it
The security of any public key cryptography (PKC) scheme relies on one property:
- It should be easy to derive a public key from a private key, but it must be infeasible to reverse that operation and derive a private key from a given public key.
With elliptic curve cryptography (ECC), this property is based on the discrete log problem, which refers to division on the elliptic curve being computationally difficult while multiplication is easy. Deriving a public key from an address is also computationally difficult, as you would have to find the preimage of a hash function, which means deriving an input from an output.
Not being able to derive a public key from an address is an important aspect when considering privacy. Using a new address for every incoming transaction makes tracking transactions much harder for an adversary.
If you were able to derive a public key from an address, you could find all addresses of a user, assuming they were derived from the same public key. This would render change addresses useless.
Now let's get into the actual process of creating a crypto wallet address from scratch.
Generating the Private Key
The purpose of a private key is to prove ownership of a UTXO-set by creating digital signatures to authorize spending.
Private keys are sometimes also called secret keys or spending keys.
When doing ECC math, the spending key is usually abbreviated with sk for that reason. A spending key comprises 32 bytes, or 256 bits of data.
This has two important implications:
- The SHA256 hash function used in most cryptocurrencies produces 256-bit outputs, which makes them a suitable candidate for private keys
- The elliptic curve used in most cryptocurrencies, scp256k1, has an order of 256 bits, which means it consumes 256-bit inputs and produces 256-bit outputs.
A private key can be represented in many formats, such as a:
- Binary string of 1's and 0's
- Base64 string
- Mnemonic phrase
- Hex string
Generating Entropy
In order for a private key to be secure, it needs to be as random as possible.
Randomness is also referred to as entropy, which is a term coming from the world of physics and chemistry describing the level of disorder in a system.
Guessing an existing private key is so unlikely no sane human would try to attempt it and stealing them is also hard assuming good operations security was employed. Exploiting the source of randomness used to create a private key and recreating it can be a viable strategy for attackers in some cases.
It's important to note that randomness should be viewed on a scale, rather than on a binary basis.
Many programming languages have a random number generation (RNG) module built in, but few of them are made with cryptographic purposes in mind.
Some, like pythons secret module, are optimized for truly random number generation. How "good" an RNG module is, depends on the source of entropy used.
It can be collected from many sources:
- The processes running on your processor
- Mouse movements
- Camera and microphone inputs
Or a mix of the above.
If you would like to go through the process of creating a private key for yourself, here is an article guiding you through the process in python.
Mnemonic Phrases
It is good practice to backup your private key in an analog format but copying and writing down your private key in one of the formats above is very error prone. In 2013 a Bitcoin Improvement Proposal (BIP) was submitted suggesting the use of mnemonic phrases to represent private keys.
"A mnemonic code or sentence is superior for human interaction compared to the handling of raw binary or hexadecimal representations of a wallet seed. The sentence could be written on paper or spoken over the telephone. This guide is meant to be a way to transport computer-generated randomness with a human readable transcription." - BIP 0039, Palatinus, Rusnak, Voisine, Bowe
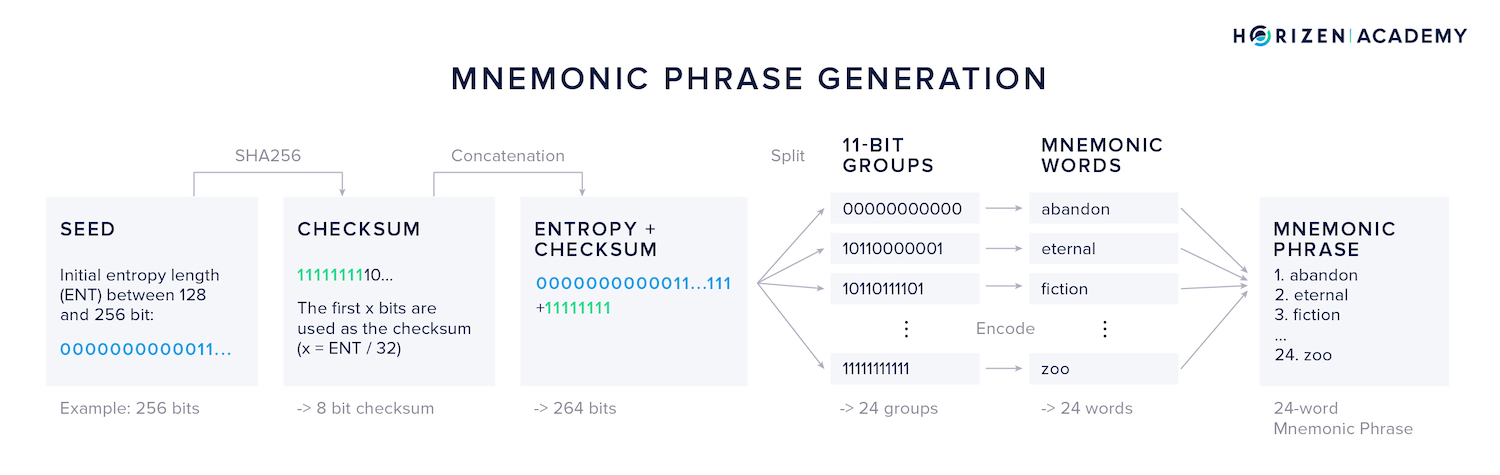
- First, randomness is generated using one of the methods described above
- Then a checksum is calculated and parts of it are linked together with the initial entropy.
- This data is split into groups of 11 bits each.
- 11 bits can represent the values from 0 to 2047
- Next, each group is mapped to a word list of 2048 common and easily identifiable words.
- Similar words such as woman/women or build/built are excluded to avoid confusion.
Deriving the Public Key
Now that we have generated a private key - - and a way to conveniently back it up, we need to derive a public key - - from it.
A scalar is something that only has a magnitude. Simply speaking, any number is a scalar.
A vector has a magnitude and a direction and is represented by a tuple of values. If we are looking at a two-dimensional plane, a vector can be interpreted as an arrow with a certain length, the magnitude, and a direction, the angle relative to the x-axis.
This means in two dimensions a vector is a tuple made of two values, a double.
To represent a vector in three-dimensional space a triple of values is needed: One for the magnitude and two for the direction, the angle relative to x- and z-axis).
Alternatively, the triple of x, y, and z-values can be used.
- Scalars are written with small letters, like -
- Vectors are written with capital letters, like -

A generator point or base point is defined for the secp256k1 curve and its coordinates are:
and
The product of your private key sk with this base point P gives you your elliptic public key, PK.
All public keys are computed based on the same generator point.
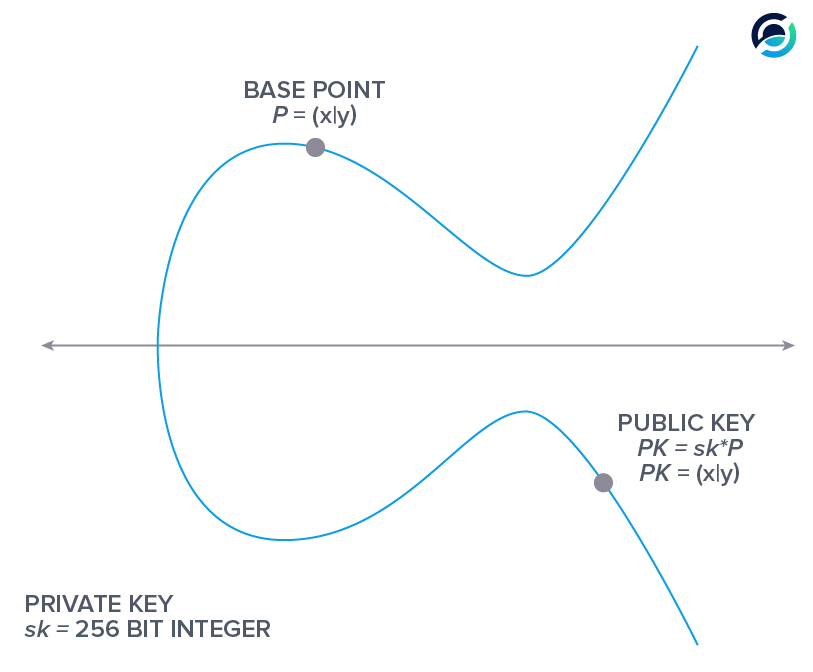
An extra byte is added to the front of your elliptic public key to give you your full public key. The extra byte depends on the specific blockchain you are generating an address for.
Compression
We already mentioned that the elliptic curve being symmetric about the x-axis is a property that makes compressing a point on the curve very handy.
For every x-value, there are only two possible y-values and they only differ in their sign.
If you throw out the y-value all together and add a byte indicating the sign of y a reduction in size by almost 50% is achieved.
Creating a Wallet Address from the Public Key
Your compressed public is now hashed twice in a row, first using SHA256 and second, using RIPEMD160.
The second round of hashing accomplishes a compression by 37.5%, from 256 to 160 bit.
What you have now is your encrypted public key.
The next step to getting your address is adding a network byte to the front.
Depending on which blockchain you are talking about this can also be two bytes. They indicate if the address is meant to be used on the production network or one of the testnets.
Horizen uses two network bytes, which causes the Base58Check encoded transparent addresses to start with zn while shielded addresses start with zc.
After we have added the network byte, a checksum is calculated and concatenated with the address. This is a security measure to prevent addresses that were corrupted during transmission from being used by a wallet.
The checksum is obtained by hashing the address including the network byte twice and taking the first 4 bytes of the result.
This checksum is then added to the end of the compressed public key.
What we have now is a valid address, but there is one last step to it.
Base58Check is a way to convert bits into alphanumeric characters, excluding the four characters 0, O, I, and l to reduce errors when copying addresses manually and proofreading them.
HD Wallets - Hierarchical Deterministic Address Generation
Most wallets today are HD wallets - hierarchical deterministic wallets.
They use a single seed or master private key which can be derived from your mnemonic phrase, to generate a number of child private keys.
This is done by adding a counter to the seed and incrementing it by one for every new private key generated.
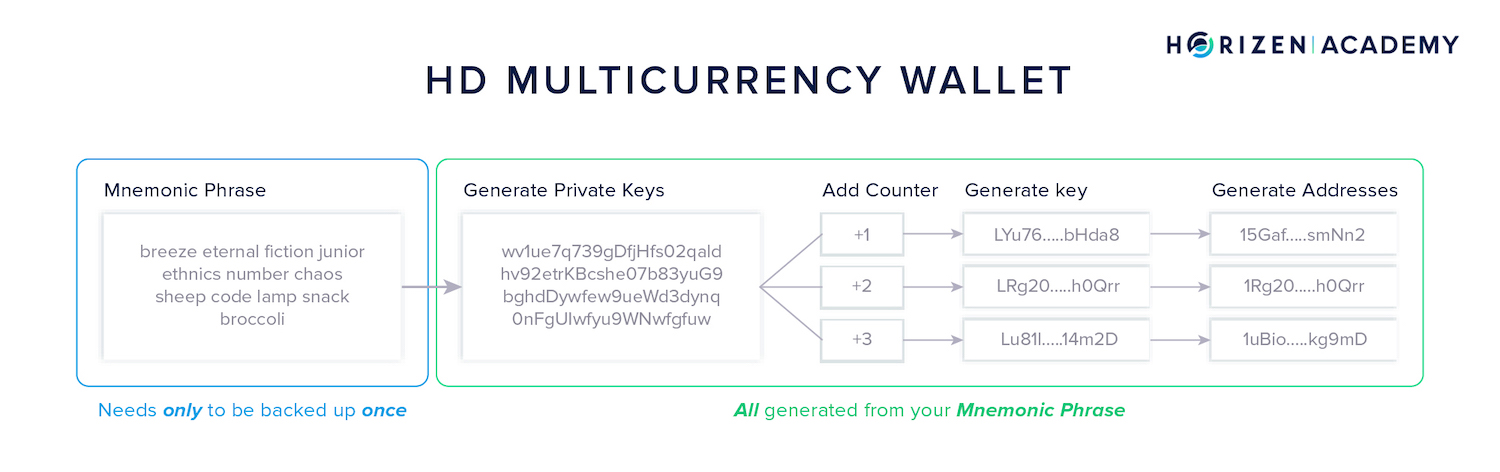
These private keys can be used for different blockchains because the underlying concept is always the same:
The private key is a source of randomness that when multiplied with the base point of the specific chain yields your public key.
Summary - Generating Wallet Addresses
To get from your private key, sk to your address you first perform multiplication on the curve with the base point P.
Next you add a leading byte depending on which blockchain the address is for and omit the y-value while adding a byte for its sign. Now two hash operations are performed in a row, SHA256 first and RIPEMD160 second to get your encrypted public key.
A network byte is added to indicate if the address is meant for the main or testnet, giving you the mainnet encrypted public key. A checksum is calculated by performing SHA256 twice and adding the first 4 bytes of that checksum to the end of the mainnet encrypted public key.
Lastly, the characters 0, O, I, and l are removed using Base58Check.