What is Proof of Work?
Proof of Work (PoW) is a concept that has been around for millennia. Andreas Antonopolous, one of Bitcoin's greatest advocates, tells this story best.
Evidence of Proof of Work can be found in many places, for example in Giza, Egypt.
The pyramids serve as a tribute to the Pharaoh, but also demonstrate Egypt's capability to build them. Visitors can immediately recognize that these monuments required a large amount of work to be built.
It's a proof of work.
Why We Need Proof of Work
Blockchain proof of work serves a similar purpose. It demonstrates the difficulty of building a blockchain by adding zeros to every block hash.
While the blockchain as a data structure is inherently tamper-evident, only PoW makes it immutable. A blockchain allows spectators to easily detect changes to records, but it doesn't prevent changes from occurring.
Proof of Work on the other hand, makes it infeasible to change any records, because an attacker would have to redo all the work that went into building the block(s).
The consensus mechanism in most blockchains comprises two components - Proof of Work and the longest chain rule.
PoW mostly provides Sybil resistance combined with an incentive system that makes honest behavior the most profitable strategy. The longest chain rule resolves disputes in case two valid blocks are found at the same time.
Voting With Computational Power
Instead of voting on proposed blocks, the chance of finding a block is proportional to a miner's relative computational power, or hash power, on the network.
This can be understood as an indirect form of voting, where the voting power of an entity is tied to the amount of electricity it spends.
“The main difference between consensus mechanisms is the way in which they delegate and reward the verification of transactions. (…) In one way or another, blockchain consensus algorithms boil down to some kind of vote where the number of votes that a user has is tied to the amount of a limited resource that is under the user’s control.” - Demiro Massessi
The limited resource in a PoW blockchain is computational power - and hence electricity.
In other Proof-of-X schemes, X can be hard drive space or the native currency of that blockchain.
Creating a Block in Proof of Work
Proof of Work is straight forward:
- First the miner collects transactions to include in the next block
- After that the miner tries hashing the block header including a nonce until the resulting hash meets the target
Step 1 - Collecting Transactions
A miner starts creating a block by including the coinbase transaction as the first transaction. The coinbase transaction is a special type of transaction that does not have any inputs, but has an output sending coins to an address controlled by the miner.
This output is worth the current block subsidy (6.25 ZEN at the time of writing) together with the transaction fees of all included transactions. The sum of the block subsidy and the transaction fees make up the block reward.

By allowing miners to include the coinbase transaction, they are incentivized to perform the computationally expensive task of producing new blocks.
When a block is produced, new coins are created to pay the miner, which means the protocol can pay for its own maintenance. Each existing ZEN or BTC started out in a coinbase transaction.
Next, miners collect new and unconfirmed transactions in their block. A transaction is called unconfirmed when it is not included in the blockchain yet.
If there are more unconfirmed transactions than what fits in a single block, miners store them in their memory pool or mempool. When blocks are full, miners select the transactions from their mempool with the highest transaction fees, calculated on a fee-per-byte basis, and include those in their block.
Miners are incentivized to maximize their revenue, and as a result, will usually choose transactions that pay the highest fee-per-byte.
Step 2 - Finding a Nonce
Now, a miner builds a merkle tree of all transactions included in the block and includes the merkle root in the block header. They add all the other necessary data, such as the hash of the previous block, and some other metadata.
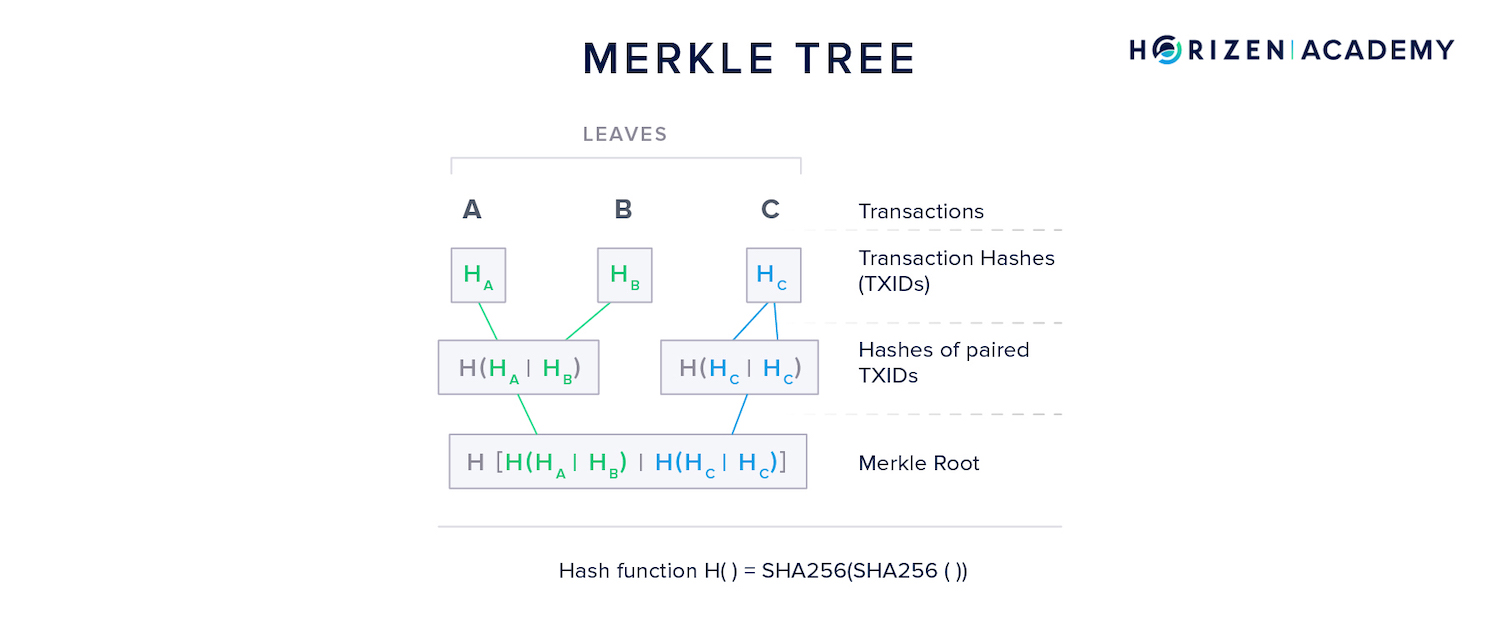
Once the candidate block is completed, the miner inserts some value in the nonce data field. The nonce - number used once - is a variable whose only purpose is to modify the block hash.
When a first nonce is inserted, the miner performs the first hash operation. They compare the resulting block hash with the current target and if it is greater than the target, they increment the nonce and performs the same steps again.
All miners do this simultaneously and are in a competition to find a nonce that produces a hash equal to or below the target.
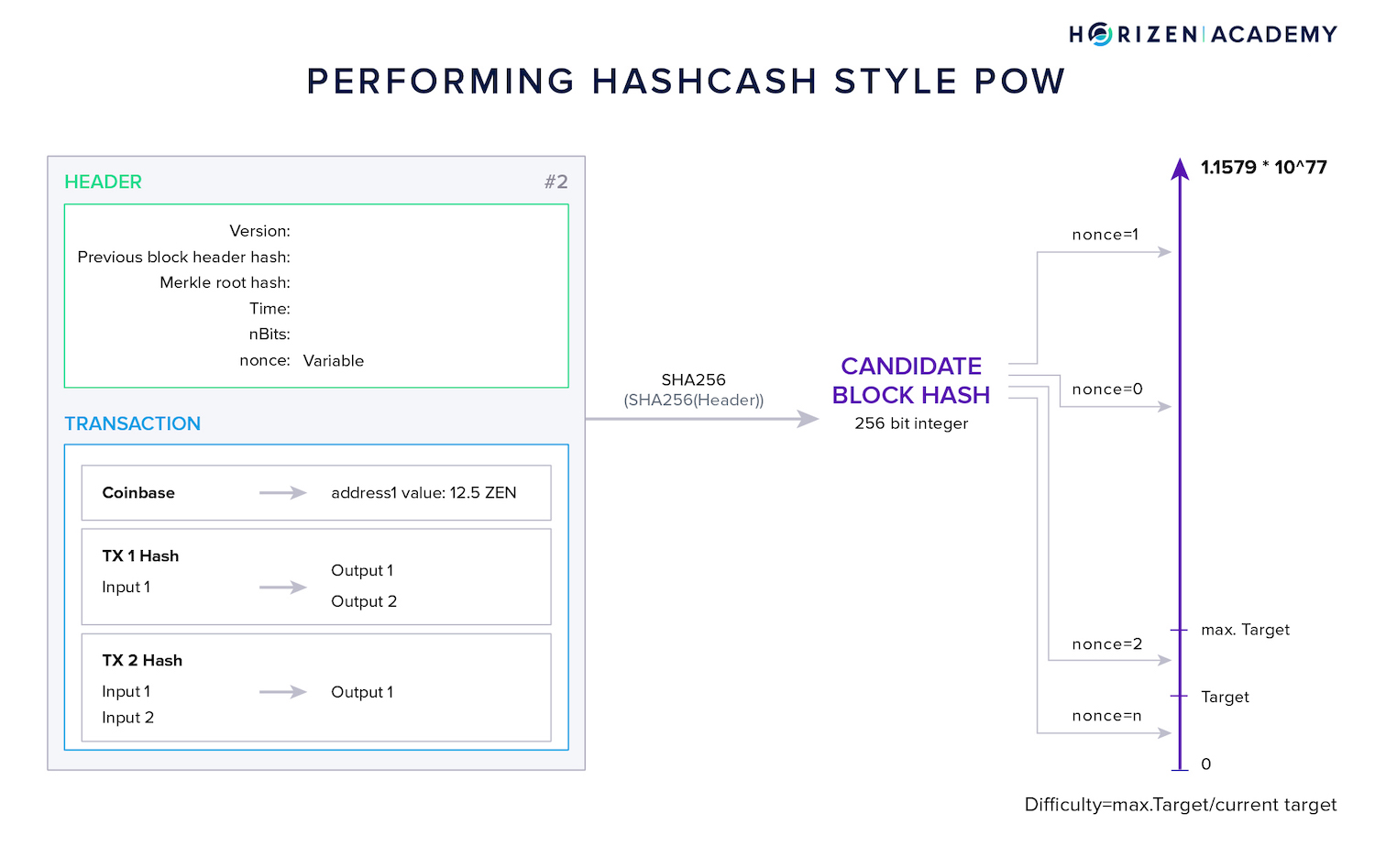
Once such a block, or better nonce, is found, the miner will broadcast the block to the network. Nodes and other miners will then check whether the block contains conflicting transactions and if the hash meets the current target.
When both criteria are met, the block is added to all copies of the blockchain. All other miners drop their current candidate block, remove the transactions that were just added to the blockchain from their mempool, and start working on a new block.
Step 3 - Meeting the Target
The terms target and difficulty are often used interchangeably. Technically, they are not equivalent though.
The target is a value that the block hash has to be equal to or below in order to be considered valid.
The difficulty is a relative measure of how difficult it is to find a hash below a given target. The highest possible target in Bitcoin is defined as:
0x00000000FFFF0000000000000000000000000000000000000000000000000000.
The difficulty is a relative measure of the current target compared to the maximum target value. The target is adjusted regularly. With Horizen, the difficulty adjustment happens with every block, in case of Bitcoin it happens every 2016 blocks.
This mechanism keeps the block time somewhat constant. When more miners join the network, hash power increases, and valid blocks are found more frequently on average. By lowering the target, and making the computation more difficult, the block time will be adjusted upwards.
Bridging the Physical and Digital World
A Proof-of-Work (PoW) system is an economic measure to remove denial of attacks and other service abuses like spam on a network by requiring work from the service requester, usually referring to processing time by a computer.
Proof of Work is the bridge connecting the digital and the physical world. It ties the voting power in a purely digital system to a costly real world resource.
Prior to PoW, consensus was only achievable with a known set of participants or a reliable communications network. Making the consensus process public left the system vulnerable to Sybil attacks. With Proof of Work, creating many Sybil identities does not provide an attacker with an advantage unless he backs them with meaningful computational resources.
While a Proof of Work system typically uses a one-way function like a hash function, a proof of work algorithm can be more than just a hash function. The most used type of Proof of Work is the Hashcash style PoW depicted in the graphic above.
Hashcash was introduced in 1997 by Adam Back as a measure against spam. Recipients would require the sender to perform a Proof of Work in order to accept the mail. While this computational overhead does not affect regular users sending a few mails per day, "professional" spam would be much harder to produce.
The principle is the same as described above: Performing repeated hashing until the resulting hash is less than some target value.
Interactive Proof of Work
In general, a Proof of Work can be one of two things:
- A non-interactive solution-verification protocol
- Or an interactive challenge-response protocol
Horizen uses both, each for a different purpose.
Just like Bitcoin and most other blockchains, mining is done via a solution-verification protocol. Miners find a solution to a problem. All nodes can verify the solution at any point in time.
Even a node that has been offline for months can verify whether or not the blocks it receives during synchronization from an untrusted are valid. It is non-interactive.
Nodes on the Horizen network are incentivized by getting a share of the block subsidy. Because we want to incentivize a robust network of capable nodes, the protocol has certain performance requirements for nodes. The requirements are checked by sending challenges to the nodes.
The response time is the basis on which nodes are assessed. This is an interactive challenge-response protocol and constitutes a different form of Proof of Work than mining.
What Constitutes a Good Proof of Work?
Some criteria for a good Proof of Work system in a decentralized blockchain with fair distribution of newly mined coins is as follows:
- Asymmetry - The Proof of Work needs to be hard to produce, but easy to verify.
- Hashing is an example of an asymmetric task. Depending on the difficulty, an incredible amount of hash operations is needed to find a valid hash, but a single operation is sufficient to verify it.
- Prime factorization in RSA is another example. It involves finding two primes whose product equals a given value.
- For the number 77 one would find 7 and 11 intuitively.
- For 54,063,013 this becomes a much more difficult task but verification can be done with any rudimentary calculator.
- Optimization Free - An optimization free algorithm means that you cannot improve the efficiency of performing that task through software or algorithms.
- Battle proven one-way functions lend themselves well for optimization free algorithms. There is no way around a trial-and-error approach. The Generalized Birthday Problem that we will explain in a bit is a well studied approach that cannot be optimized.
- Amortization free - This means that a miners economies of scale cannot render all other mining pools irrelevant.
- In the best case scenario it wouldn't matter if a miner runs one miner or a million. This is obviously not entirely practical. Cooling, electricity, and facilities to set up mining equipment will always enable large miners to operate at a better margin than smaller operations. The PoW algorithm itself should not allow this advantage though.
- Independently Tunable Parameters: Certain parameters of the "puzzle" miners are attempting to solve should be easy to adapt. One of those parameters is the target or difficulty we discussed above.
- By being able to tune this parameter depending on miner activity, the protocol can attempt to keep the block time constant.
Let' take a look at the asymmetric property first. It means the task has to be computationally expensive to perform but easy to verify.
Computational Hardness
Proof of Work schemes always involve a computationally hard problem.
The term computationally hard can further be broken down into three classes:
- Network-bound refers to the available bandwidth
- CPU-bound refers to the required processing power
- Memory-bound refers to storage capacities, usually RAM
Network-bound Algorithms
All schemes have certain advantages and shortcomings. Network-bound approaches are less hardware intensive and rely more on operational expenditures than capital expenditures. At the same time they are more vulnerable to attacks such as Denial of Service (DOS).
Network-bound algorithms rely on bandwidth, which relies heavily on the physical location of the miner.
CPU-bound Algorithms
The CPU-bound approach gives large players with capital a decisive advantage. Proof of Work usually involves performing a single computational task many times in a row.
Special hardware, so called Application Specific Integrated Circuits (ASICs), can be built for CPU-bound tasks. They sacrifice versatility for efficiency and thereby offer an advantage in performance.
Because ASICs are domain specific and expensive, most users don't have access to them.
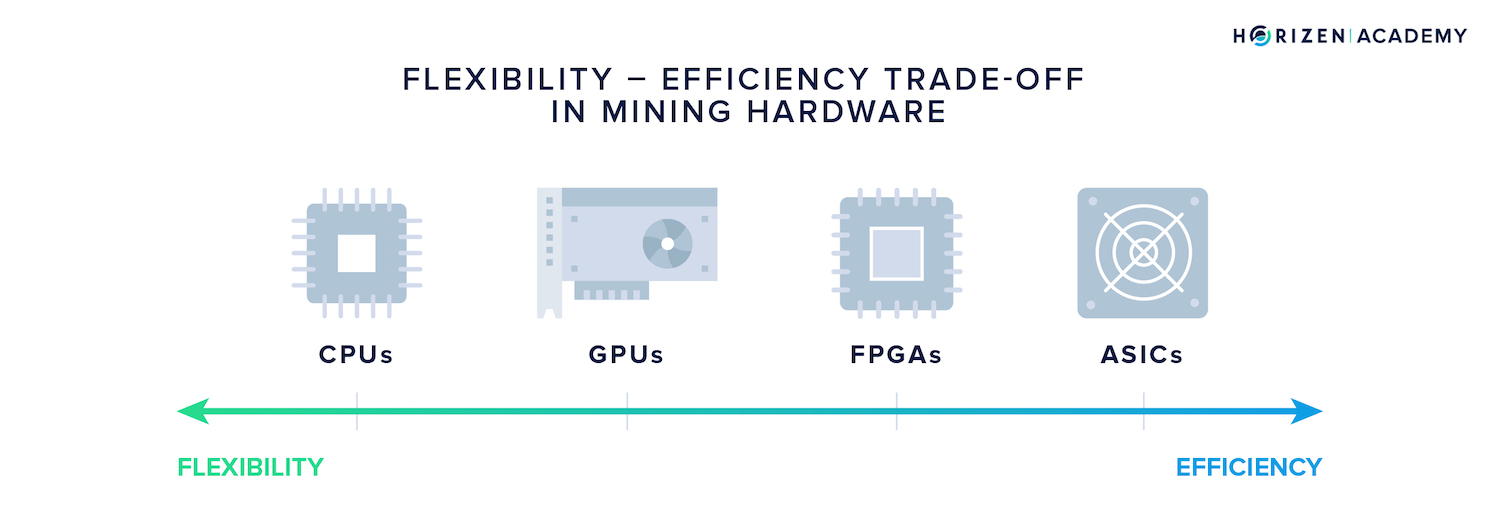
Memory-bound Algorithms
It was long thought that memory-bound puzzles were less prone to hardware optimizations. The Equihash algorithm for instance was thought to be ASIC-resistant for a long time, but things turned out differently.
The memory-bound approach suffers from an obvious flaw: if you could find a way to store all that data in memory once, using a lot of expensive DRAM, but then share this data across a large group of inexpensive processors, you would effectively share the cost across a large number of processors and thus undermine the supposed difficulty of the problem. And this is exactly what has happened recently." - Jeffrey Emanuel
The author is referring to the emergence of ASIC miners for the Equihash mining algorithm. Most PoW schemes are CPU-bound. Some algorithms previously referred to as ASIC resistant, are memory-hard, but rarely memory-bound.
This means they require a lot of memory to be performed, but once that amount of memory is available, speed improvements are realized through increasing the processor performance rather than adding more memory.
As we mentioned above, this design didn't keep them ASIC resistant for long. It is always possible to build more efficient hardware, compared to commodity hardware, for a given problem, at the expense of versatility.
An Edge-Case - The Tangle
An interesting side note is that bandwidth is a consideration in the IOTA Tangle, designed for use in IOT devices performing many micro transactions. The Tangle is a Directed Acyclic Graph (DAG) consisting of individual transactions.
Each transaction has a small proof of work attached. The protocol's security is based on the assumption that honest participants will make up the majority of transactions and also make up the majority of computational power.
If Tangle was widely adopted for micro-payments in the IOT sector, computational power would secure the network and constrain the bandwidth of a single attacker. It would be very hard to amass more bandwidth as a single entity than all honest devices combined. In order to broadcast a majority of transactions, one needs a majority of computing power and bandwidth in this setting.
A DAG's security can have both CPU-bound and network-bound components.
Metrics to Assess Computational Hardness
There are two different metrics to rate the difficulty of a computational task:
- Time complexity
- And Space complexity
Time complexity refers to how many additional computations result from an increase in the input to a function. With infeasible time complexity, slight increases in input size will result in an exponential increase in time for the computation to finish.
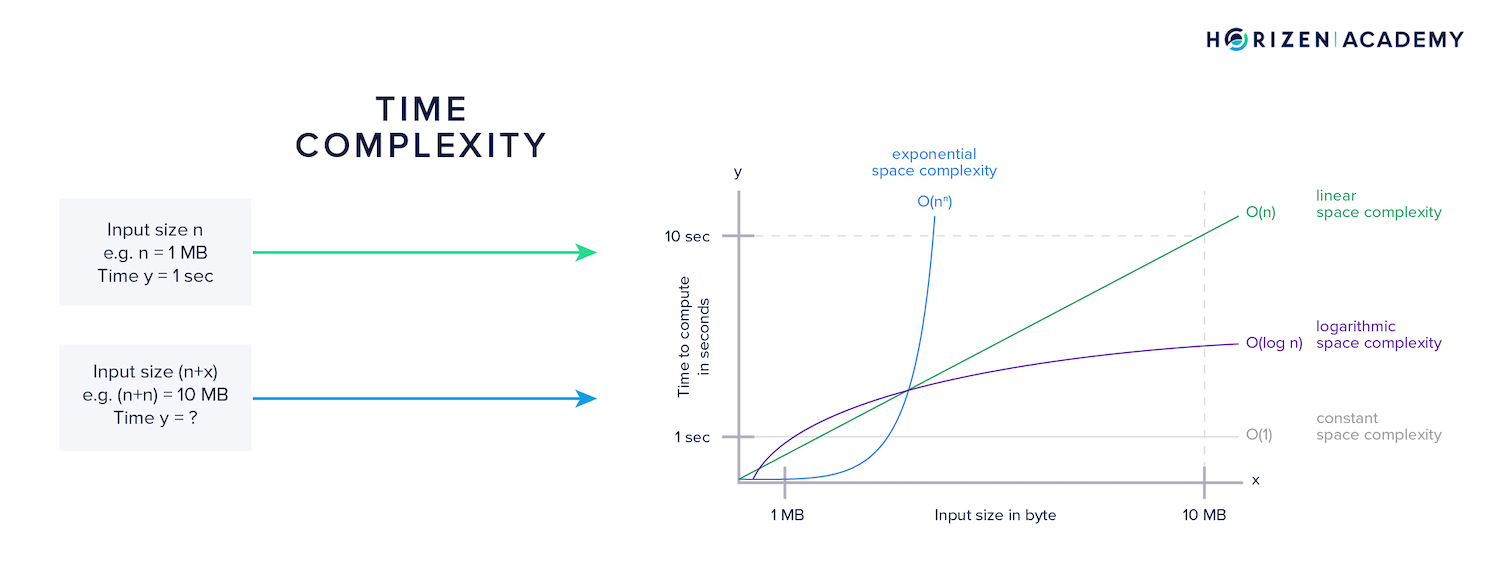
Space complexity refers to how much additional memory is needed when the input to a function increases. With infeasible space complexity, the memory requirements quickly exceed all hardware limits.
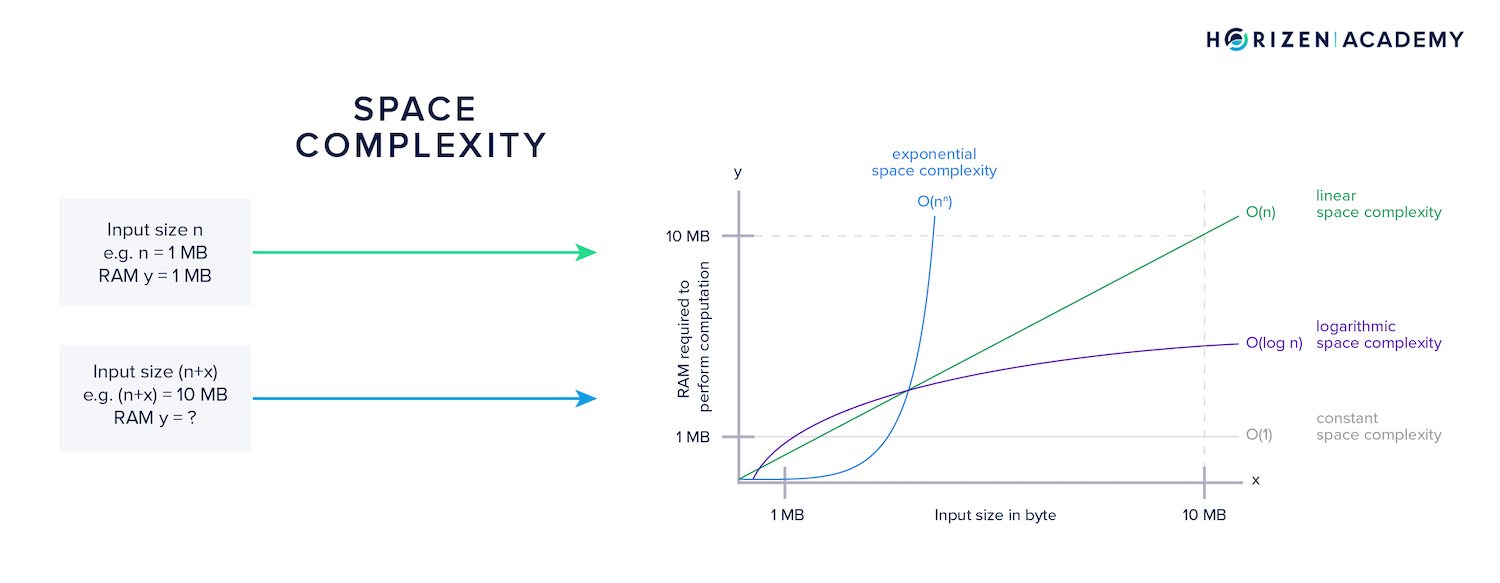
An algorithm designed for a Proof of Work has to make tradeoffs between the two. When we talked about CPU-bound algorithms, we meant those with a high level of time complexity. On the other hand, memory-bound algorithms have a high level of space complexity.
The Birthday Problem in POW
Let us take a look at the parameters of a PoW scheme so that we better understand how to tune it. The most intuitive parameter to understand is the target or difficulty.
Because cryptographic hash functions map their inputs evenly across the output range, lowering the threshold a hash value has to meet makes the task more difficult. The more hash power is on the network, the lower the average time until such an input is found.
Without a difficulty adjustment this would result in shorter block times. Lowering the target increases the block time.
There are much more complex PoW algorithms though. One of the more widely used ones is Equihash, which is based on the Generalized Birthday Problem and used by the Horizen blockchain.

The birthday problem describes an interesting property regarding a group of people and their birthdays. In a group of 367 people, the probability of two of those people sharing a birthday is 1, because there is one more person than there are days in a leap year.
However, with just 23 people in the group, the chance of two of them sharing a birthday is already at 50%, while it reaches 99.9% with just 70 people.
The Generalized Birthday Problem

The generalized birthday problem refers to the difficulty of calculating those probabilities in a more general context.
We define a time period of d days, and ask how many people n do we need to have a 50% likelihood of a birthday coincidence.
The Multi-Dimensional Generalized Birthday Problem

Next, we can increase the number of dimensions for the problem.
You can see how the problem becomes more dimensional when you look at the function in the bottom-right corner of the graphics in this section. Calculating the probability p of a birthday coincidence is a function of one variable in the first case, namely the number of people n.
For the generalized birthday problem the function is two-dimensional and depends on the amount of people n and the time period d.
We can further increase the dimensionality of the problem by looking at k groups of \(n_k\) group members instead of a single group, for instance two groups of \(n_m\) men and \(n_w\) women.
In this case the multi-dimensional birthday problem comes down to calculating the likelihood of a man and a woman sharing a birthday.
Wagner's Algorithm
Starting from the generalized birthday problem, David Wagner devised an algorithm - the Wagner's Algorithm - to compute those probabilities for even more complex setting with k dimensions (groups of people) and n-bit settings (days).
The algorithm was found to be hard on time and space. The time and space complexity trade-off can be adjusted by the parameter k.
This means, very loosely speaking, that if one uses the generalized birthday problem for a PoW algorithm, one can make it more CPU or memory intensive depending on the number of groups k a birthday collision is calculated for.
To give you an idea: Horizen has implemented Equihash with the parameters n=200 and k=9.
The miners goal in Equihash comes down to finding a solution to the multi-dimensional birthday problem, that meets a certain target.
Other Computationally Hard Problems
Some other examples of computationally hard problems used to create a Proof of Work include finding prime numbers and solving the Traveling Salesman Problem.
In Primecoin, the PoW task is to find prime number chains like Cunningham chains and Bi-twin chains where primes roughly double or follow a specific sequence. The Cuckoo Cycle algorithm by Tromp et al. is based on graph theory.
It comes down to the Traveling Salesman Problem and is implemented in Grin and æternity.
Another interesting concept was presented with ProgPoW. Its algorithm is designed to match already available hardware to reverse the scenario that has played out in the past.
Those companies with the largest budget were able to bring specialized mining hardware for a given algorithm to market first. In the case of ProgPoW the algorithm was designed with existing hardware in mind rendering advantages in R&D budgets for large manufacturers irrelevant.
POW Incentives
Proof of Work in cryptocurrencies has an intricate but ingenious built-in incentive system. Miners are rewarded with a block reward which consists of the fixed block subsidy as well as the transaction fees attached to each transaction.
On a high level, miners are rewarded with a ledger entry for spending real world resources in the form of electricity. PoW therefore builds a bridge between the digital and the real world.
POW Vulnerabilities
51% Attack
PoW also has some vulnerabilities - no system is perfect. It is hard to achieve Byzantine Fault-Tolerance in the first place, let alone tolerating a large share of byzantine actors. Simply speaking, Byzantine behavior mostly refers to malicious behavior.
Building a working system with more than one third of the network acting Byzantine took many years. However, combining Proof of Work and the longest chain rule can tolerate malicious hash contributions of up to 49%.
If an attacker controls the majority of hash rate, he can reliably perform a 51% attack. This means he can create blocks faster than the honest partition of the network.
According to the longest chain rule, the honest and rational actors of the network will accept the malicious chain as valid, once it is broadcast. This allows the malicious actor to perform double spends. The attacker spends coins in a transaction that is included in the honest chain. He then rewrites this part of the transaction history with his own blocks, which don't include his spending transaction.
Once this sequence of blocks is broadcast and accepted by the other network participants he is in control of his coins again and can spend them a second time - a double spend.
Horizen has a mechanism in place to make it significantly harder to perform a 51% attack. We introduced a block acceptance delay in relation to the amount of time the block has been withheld from the public network.
This can be best described with a short example:
In the graphic above, the malicious chain was broadcast with a delay of 4 blocks (block 39 - 42). The delay is the amount of honest blocks mined on top of the last common block before the fork. Horizen's block acceptance delay modifies the longest chain rule.
The malicious chain is not immediately recognized by the other nodes. Instead, a penalty is calculated based on the delay n, using a delay function DF. Let's consider a rather simple delay function:
For a 4 block delay, an additional 10 confirmations are required for the rest of the network to accept the fork. For a short delay of one block time, the delay function gives a penalty of one block - which is equivalent to the longest chain rule. In this case only one additional confirmation is needed to break the tie between two blocks of the same height.
For long delays, say 20 blocks, the penalty would incur an additional 252 blocks of confirmation before the malicious chain were to be considered valid. Waiting for 20 confirmations would mean a reasonable confirmation time of 50 minutes.
This makes 51% attacks and the resulting double spends much harder. In practice, there is a 4 block tolerance implemented on Horizen, so the delay function is calculated based on the actual delay minus four blocks.
DDos Attacks
Another potential threat is (Distributed) Denial of Service or (D)DoS attacks, where a malicious actor tries to slow down or halt the network by sending a large number of messages in order to limit the network's capacity. In blockchain, the attacker would replace messages with transactions to flood the network. While (D)DoS attacks can certainly harm the system, they can't affect the integrity of the ledger. It doesn't make much sense for a rational actor to spend resources on a DoS attack, since the attacker has to pay transaction fees as well, if the only effect is a temporary slow down of the network.
Sybil Attacks
Lastly, PoW is inherently Sybil-resistant. An entity can create as many identities or nodes on the network as they like, but without a substantial amount of computing power those nodes cannot affect the ledger integrity. Therefore creating multiple identities offers no benefits over gathering hash power in a single mining node.