What are Consensus Mechanisms?
A Consensus Mechanism is the set of protocols used by nodes on a blockchain or distributed ledger system to come to an agreement on the current state of the network: the most up to date account of wallet balances and token transfers on the ledger.
Today, the most popular consensus mechanisms include:
- Proof of Work - PoW
- Adopted by Bitcoin and Horizen
- Proof of Stake - PoS
- Adopted by Ethereum, Cardano and Tezos
- Delegated Proof of Stake - DPoS
- Adopted by EOS
- Proof of Authority - PoA
- Adopted by VeChain
- Proof of History - PoH
- Adopted by Solana
- Practical Byzantine Fault Tolerance - pBFT
- Adopted by Hyperledger
- Directed Acyclic Graphs - DAGs - ‘Gossip Protocol’
- Adopted by Hedera Hashgraph
Consensus mechanisms play a critical role in determining how efficiently a blockchain can update its state and process transactions while remaining decentralized.
Horizen EON is our first public proof-of-stake sidechain and a fully EVM-compatible smart contracting platform that allows developers to efficiently build and deploy dapps on Horizen, while fully benefiting from the Ethereum ecosystem.
The Scalability Trilemma
This challenge is commonly referred to as the Scalability Trilemma, a term coined by Ethereum founder Vitalik Buterin which described the tradeoff that developers make between scalability, decentralization and security when designing a blockchain. It is referred to as a trilemma because in theory a blockchain cannot achieve scalability without compromising decentralization or security.
A network with fewer nodes requires less validators to confirm transactions, which means it takes less time for a transaction to be added to the next block in the chain. However, fewer nodes leads to more centralization, which means the network can be significantly impacted if even just 1 or 2 of the nodes were to go offline, making the system more fragile.
When it comes to solving the scalability trilemma, the type of consensus algorithm adopted by a blockchain network is equally as important as the number of nodes required to achieve consensus on the network.
One way to think about a consensus protocol is as a unique language or way of speaking that nodes must use to communicate with each other about the current state of reality in the digital realm. Most importantly, this communication method must be designed in such a way that it allows consensus to be achieved quickly while still being resistant to censorship or manipulation from bad actors.
Consensus Mechanisms Explained Through the Telephone Game
Imagine, for example, a group of kids sitting in a circle playing the telephone game.
The goal is for a message to travel from one person's ear to the next and go all the way around the circle without being changed. Each person's responsibility is to carefully listen to the message and then deliver it to the next person clearly so that it is not misinterpreted by the time it reaches the last person's ear.
How do we solve the problem of getting the message across in a timely manner without someone mistakenly or intentionally changing it?
If we use the telephone game as an analogy for consensus mechanisms and the scalability problem, we can see how it is really about figuring out ways to coordinate a group of participants acting on their own self interest to agree on a single message that can be correctly communicated to everyone in the group.
Taking this analogy a step further, we can implement certain rules in the telephone game in order to ensure that the message is delivered as it was intended and that each person passing on the message is less incentivized to manipulate it.
- First, when a message is passed from person A to B to C, we could require person C to repeat the message they received from person B back to person A.
- Similarly, when a message is passed from person C to D to E, we could require person E to repeat the message they received from person D back to person C, and so on.
- Second, we could require each person to put $10 in the middle of the circle, which they will lose if it is confirmed that they intentionally or accidentally shared the wrong message to the person next to them.
- Alternatively, each person could be required to solve a mathematical problem that would take roughly 5 minutes before they could pass on the message to the next person.
- Lastly, everytime a message is successfully passed across to everyone, one person will be chosen at random to receive $5.
These rules roughly describe the process in which a new block is added to the chain under a proof of work or proof of stake consensus mechanism:
- A transaction is validated and then shared amongst other nodes
- Each node performs some arbitrary computation or stakes something of value to deter dishonest behavior when validating and sharing the transaction
- Then for each block of transactions added to the chain, a reward is given to a single node based on a deterministic or probabilistic order
The more redundancies that are put in place before a message can be transmitted between nodes, the harder it is for bad actors to manipulate the message.
On the other hand, reducing the redundancies and number of participants needed to communicate a message enables you to get more messages across in less time but also creates opportunities for bad actors to distort the message for their own ends.
The key to solving the scalability trilemma is to figure out a method of communication between nodes that is fast and cheap, yet filled with necessary redundancies that can deter manipulation.
Increasing Block Size for Scalability?
The size of a block has been the topic of much debate ever since the birth of Bitcoin in 2009.
Even today, many people still believe the quickest way to scale a blockchain network is to simply increase the amount of transaction data that each block can store, thereby enabling more transactions to be processed each second and increasing the speed of the network.
The problem with this assertion is that it does not come without compromising decentralization.
On a proof of work blockchain, when the size of the block increases, the amount of energy a node needs to validate transactions and store all the data in each block also increases. This creates a situation where miners are forced to increase their energy output in order to remain profitable when validating larger blocks. This naturally leads to weaker miners being weeded out as they can no longer afford to operate at a high level given the increased energy requirements.
Fewer miners leads to consolidation of hashing power by the strongest and most resourceful miners, which subsequently leads to centralisation of the network. The same thing applies to proof of stake blockchains, where an increase in data storage requirements will make it more costly for the average validators to validate transactions or store a full record of the chain using a basic laptop.
The debate around block sizes hit its peak in 2017 during a period known as the ‘Block Size War’ where the Bitcoin community became so fractured over the issue of whether to increase the size of blocks that it led to a hard fork and the creation of Bitcoin Cash.
Comparing Consensus Mechanisms
Walking the fine line between having too many nodes, too much data per block or too many built in redundancies needed to add new blocks to the chain and the alternative, which is just another centralized database, is the complex and delicate balance that blockchains attempt to maintain using different methods of consensus.
Each approach has its unique pros and cons which we have highlighted below:
Proof of Work
In a Proof of Work consensus mechanism, miners contribute computing power to solve complex mathematical puzzles in order to produce a new block and earn a mining reward.
Proof of Stake
Proof of Stake requires validators to stake their tokens into a smart contract in order to validate transactions. A randomized process is used to determine which validators will get to produce the next block.
Proof of History
With PoH, nodes create a real time snapshot of events and transactions as they occur using a recursive verifiable delay function. Snapshots are linked together to form a chronological chain of events and transactions on the blockchain.
Each node has a cryptographic clock that is built in to help the network agree on the ordering of events and time of transactions.
Delegated Proof of Stake
In Delegated Proof of Stake, users stake their tokens and vote in delegates who are in charge of creating new blocks under the same PoS model.
Proof of Authority
The Proof of Authority mechanism uses reputation as the basis for achieving consensus. Instead of staking coins, validators stake their reputations. This method is primarily used by private blockchains where identities are already verified.
Practical Byzantine Fault Tolerance
With pBFT, blocks are validated by special “ordering” or “leader” nodes which are regarded as final and true. This mechanism is designed for private consortium blockchains where members are partially trusted.
Directed Acyclic Graph
DAG’s are a type of data structure used on distributed ledger technologies. DAG’s enable the use of a gossip protocol, which allows nodes to achieve consensus by broadcasting information to other nodes in a random manner until broad consensus is achieved about the state of the ledger.
| Consensus Mechanism | Proof of Work - PoW | Proof of Stake - PoS | Proof of History - PoH | Delegated Proof of Stake - DPoS | Proof of Authority - PoA | Practical Byzantine Fault Tolerance - pBFT | Directed Acyclic Graph - DAG |
| Used By | Bitcoin | Ethereum, Polygon, Cardano, Avalanche | Solana | EOS, Tron, Polkadot - Polkadot uses Nominated PoS or NPoS which is similar | Vechain | Hyperledger | Hedera Hashgraph, IOTA |
| Layer 1/2 Scalability | L2 - Lightning network | L2 - Sharding, Rollups | L1 | L1 | L1 | L1 | L1 |
| Transaction Throughput - Transactions per Second | 7-30 tps | 7,200 tps | 1,446 live tps | 2,800 tps (EOS),1,000 tps (Polkadot) | 10,000 tps | 3,000 tps | 10,000 tps |
| # of Validates/Nodes | 4,634 Ethereum nodes.10,203 Bitcoin nodes. | 100 Polygon Validtors | 930 Solana Validators | 21 EOS Validators27 Tron Validators | 101 Vechainm Validators | Dependent on # of consortium members | 18-20 Hedera Validators |
The blockchain scalability trilemma has influenced the design of virtually every major blockchain protocol that exists today. The belief that a blockchain can be faster, cheaper and more malleable, while retaining security and decentralization has served as fuel for talent and capital to flow into this industry .
The primary goal- creating a scalability-driven path to mainstream adoption.
Horizen’s Approach to Consensus
Horizen’s core product Zendoo makes it easy to be consensus agnostic. It provides a sidechain SDK that enables businesses and developers to create custom sidechains on top of the Horizen mainchain. This in turn means that they can leverage the most secure form of PoW used by the mainchain.
Each custom blockchain can have its own unique consensus mechanism. Additionally, custom blockchains can communicate and exchange value with other blockchains in the Horizen ecosystem using its novel Cross-Chain Transfer Protocol, or CCTP.
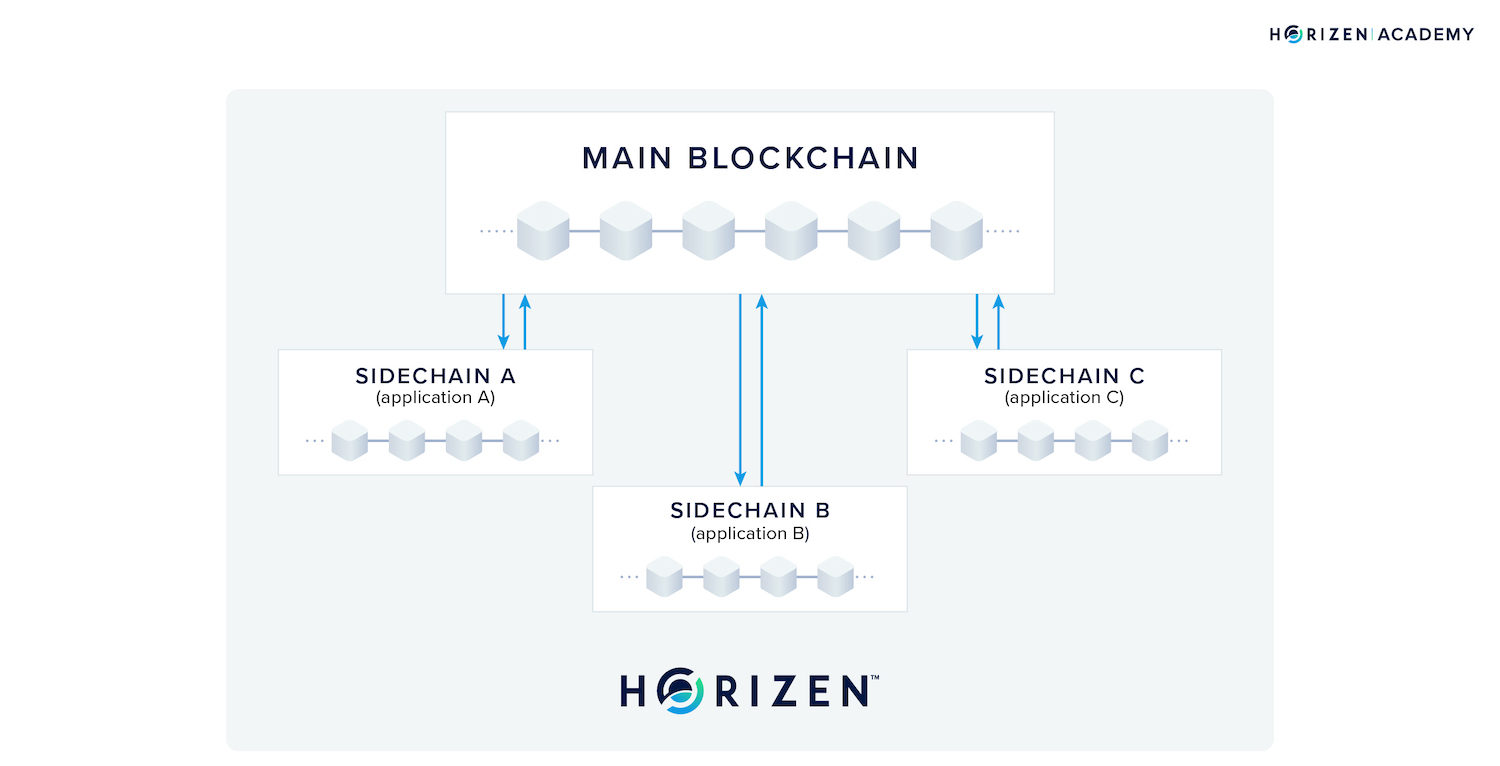
What this means is that a developer who is looking to build both an exchange and an identity storage and authentication solution, does not need to compromise security to achieve high transaction throughput, nor speed to achieve decentralization.
Instead, they can choose to set up a PoS blockchain for one solution that is interoperable with another blockchain that uses PoW for storing and authenticating identities. In fact, you can technically build on top of as many sidechains with different consensus mechanisms as you want. This gives you a greater capacity to scale without the common challenges of network congestion that occur on single blockchain applications.
Additionally, you can choose between a public permissionless sidechain and a private permissioned sidechain, with the ability to exchange value between chains. Therefore, you can leverage the security of a public blockchain while retaining the privacy of data transmitted to the public chain through the use of zero-knowledge proof cryptography. These features are what enable developers to build applications that aren't just blockchain agnostic, but also ‘consensus agnostic’.
Developing applications that are blockchain agnostic, meaning your application is not limited to one blockchain but operates on multiple chains at once, has been standard practice in the industry for years.
However, if blockchain agnosticism means only being able to launch your application on Ethereum, Cardano or Solana - 3 blockchains that each use a variation of proof of stake - then this represents a clear limitation on your ability to be flexible and adapt to future innovations.
Horizen sees that what differentiates one blockchain from another is mainly the consensus mechanism. Additionally, the true path to blockchain scalability resides in consensus agnosticism. So it becomes clear that most blockchains are ill-equipped to handle a world where developers want to pick and choose between different methods of consensus without incurring massive switching costs.
It is currently very difficult to migrate from a PoS blockchain to a PoW one, or to a distributed ledger built using a DAG-based protocol and achieve that without an infrastructure that is built to offer such flexibility and modularity.
The Horizen network is built to cater to all forms of consensus mechanisms. We believe in empowering developers and entrepreneurs to push the boundaries of what is possible for blockchains and distributed ledger technologies through the creation of hybrid consensus solutions.