What is Public-Key Cryptography? - PKC
Since the goal of the original blockchain design was to enable a new and fair form of money, it would be great to be able to actually own money in this system, wouldn’t it? There must be a concept of identity to have ownership on the blockchain - you cannot have ownership if there is no representation of the owner.
Public-Key Cryptography makes it possible to represent identity on the blockchain. It is the second cornerstone of blockchain technology besides hash functions.
While hash functions are used to verify the authenticity and integrity of data, public-key cryptography is used to verify ownership on the blockchain.
Let’s take a step back and start from the beginning.
What is Public-Key Cryptography?
The basis of public-key cryptography is:
- Private keys
- Public keys
- Addresses
- and Digital Signatures
When you own some cryptocurrency, the blockchain contains a record that there are some coins associated with your public key.
- You must provide a digital signature to authorize the spending of those coins.
- You can only provide this digital signature if you are in the possession of the private key that corresponds to the public key.
Public-key cryptography, also known as asymmetric cryptography, to verify ownership. Every user creates two keys when he joins the network, a public, and a private key.
The public key is like an address, in that you give it to anyone who wants to send you money. If a friend wants to send you some cryptocurrency, you will give them your public key.
The private key is like a password, in that it can access your money and spend it, similar to how someone with your email password can't log into your account and send emails in your name.
It is important to protect your private keys. If someone gets their hands on your private keys, they can steal your money.
Elliptic Curve Cryptography
To understand how your keys and addresses work together, we must introduce Elliptic Curve Cryptography (ECC) first.
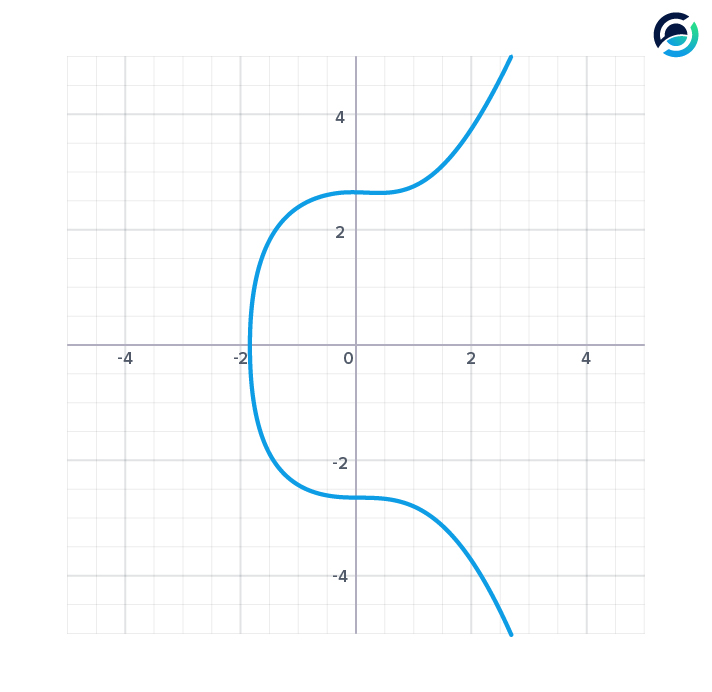
There are different ways to build a public-key cryptography scheme. Bitcoin and most other cryptocurrencies use Elliptic Curve Cryptography (ECC).
Bitcoin, Ethereum and many other currencies use a curve called secp256k1 and it looks like the one above. The equation for this curve is y^2 = x^3 + 7.
What make elliptic curves useful is that you can do math with them, and the math you do on the curves has some special properties.
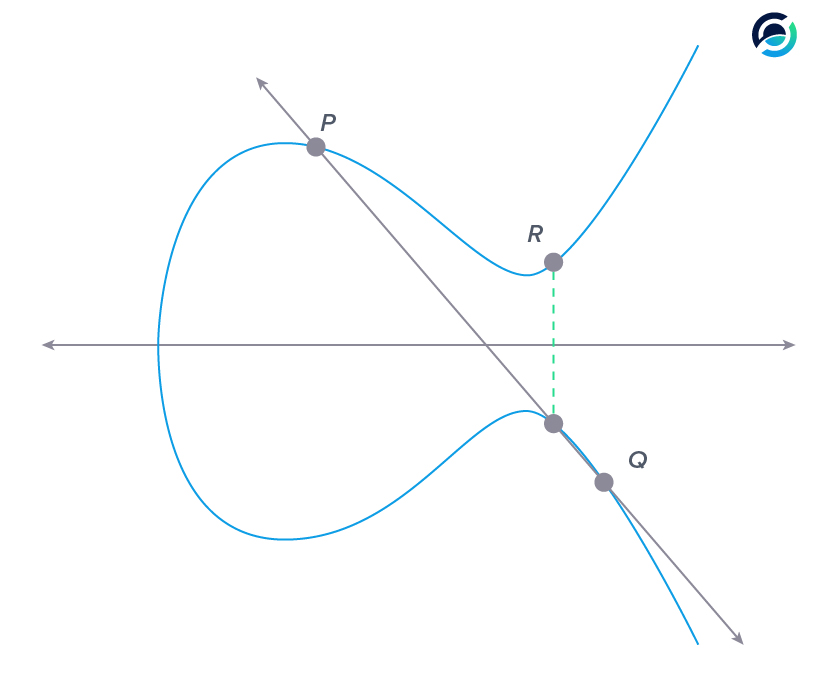
The graph above shows an example of adding two points on the curve together.
When we want to add points P and Q together, we first connect them with a straight line. This straight line will intersect with the curve at a third point.
Now we must project the third point onto the other side of the x-axis (multiply the y-coordinate by -1) and we get the sum of point P and Q: R. The key takeaway is that the sum of two points on the curve is a third point on the curve and it is easy to compute.
When we want to multiply a point on the curve we must add it to itself.
To multiply point P by two we add it to itself once. In this case, we can't really connect two points, so we go for the tangent line, the one with the arrows.
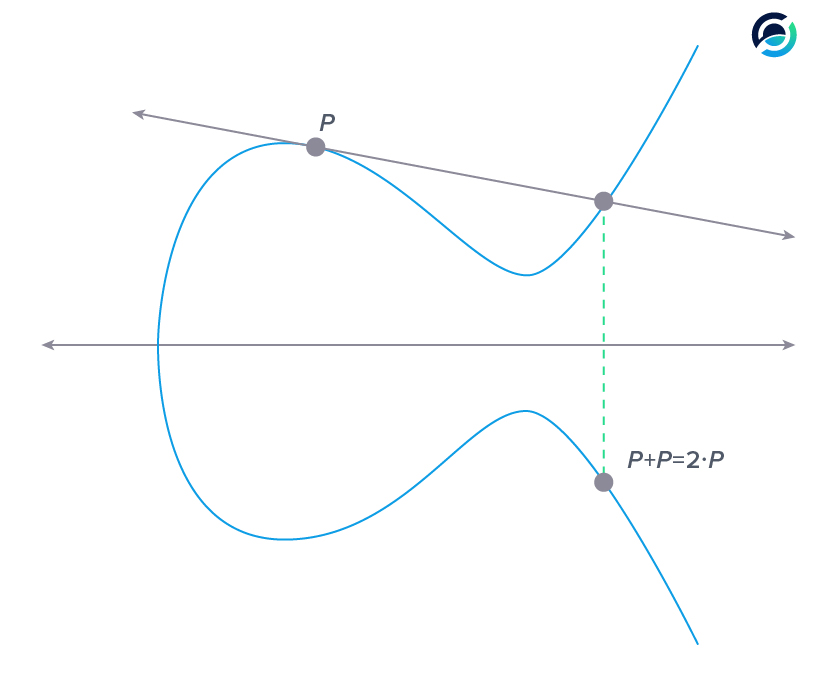
Why the tangent line?
- If you look at a random point close to P (the lightest gray), connecting the two points will result in the lightest gray line.
- Moving this point closer and closer towards P (from light to dark) brings the connecting line closer to the tangent line.
- The closer two points on the curve get, the closer their connecting line resembles the tangent until they become the same.
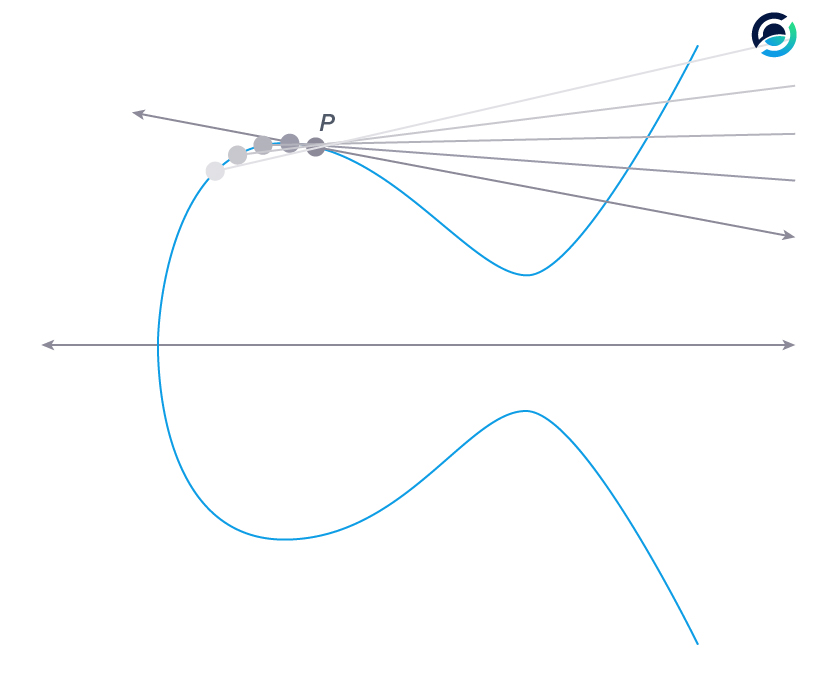
Now the addition to itself is easy. We take the intersection of the tangent line with the curve once again and project it onto the other side of the x-axis - easy.
If we want to multiply P by 3, we need to add P and point (P + P) together. To multiply P by four we can add point (P + P) to itself and so on.
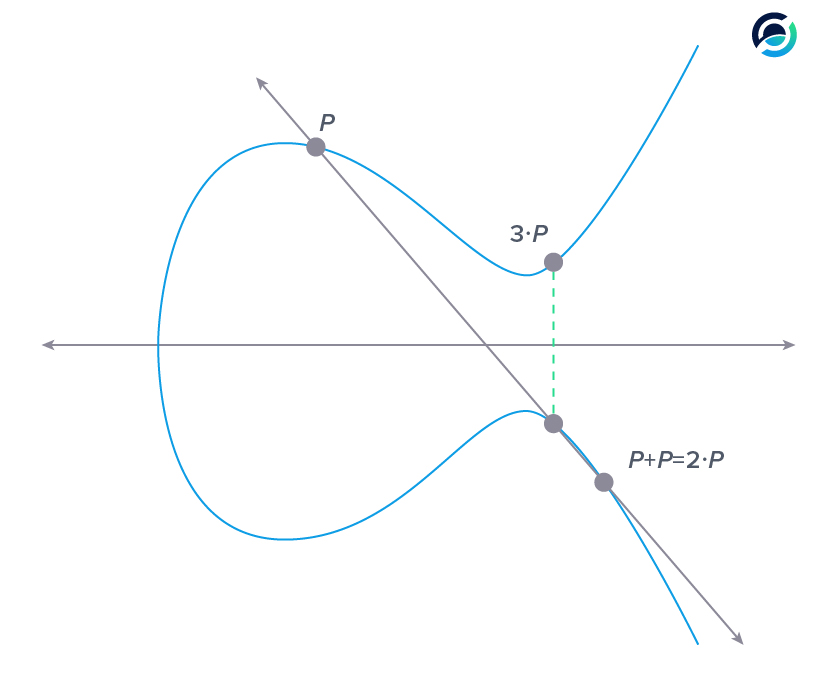
The key takeaway is that multiplying a point is an easy task - it is just adding points to themselves. The interesting part is that division on the curve is a computationally hard problem.
There is just no algorithm to calculate how many times P was added to itself or in terms of multiplication by what number it was multiplied in order to get to a certain point. This is already enough to understand the basic concept of public-key cryptography based on elliptic curves.
Private Key
When you set up a wallet, the first step is generating your private key. Your private key is a very large random number, 256 bit long. This number is so large you could assign almost every atom in the observable universe a unique private key.
Your private key should be as random as possible. Creating random numbers is harder than it might sound, but this step is crucial to the safety of your funds.
Public Key
Next, your public key is derived from the large, random number you have generated as your private key. This is where we need to multiply points on the curve. As we said earlier, adding points together on an elliptic curve is straightforward. Bitcoin uses a base point on the curve for every key pair.
Its coordinates are:
and
This base point is now added to itself as many times as your private key dictates. If your private key was the number “3”, then you would perform the calculation we just demonstrated above. If you add the base point to itself as often as your private key says (private key * P) you get your public key.
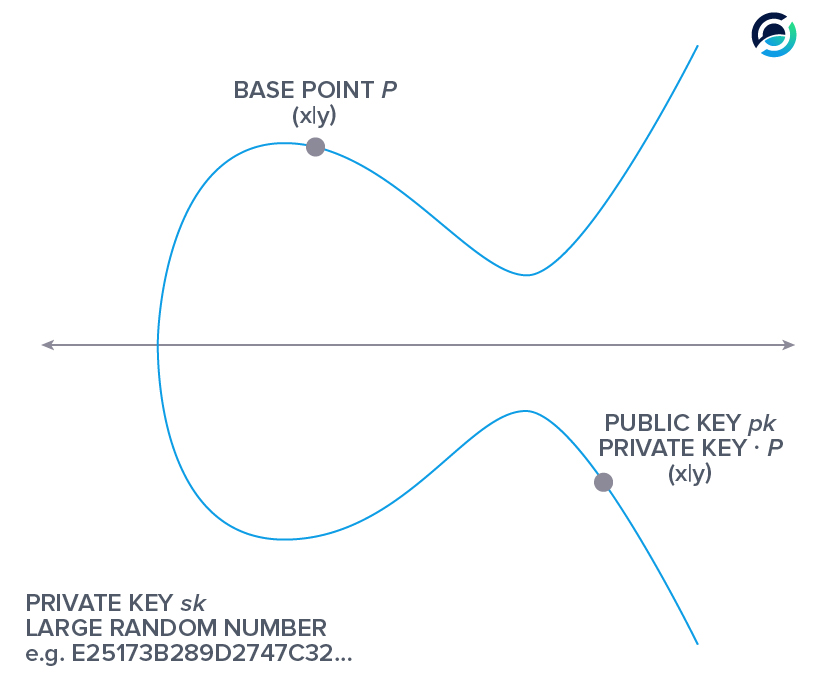
To recap:
Your private key is a large random number. Your public key is a point on the elliptic curve that you get when you multiply the base point P with your private key.
A property that is necessary for any public-key cryptographic scheme, is that it is computationally infeasible to derive the private key from the public key. It is easy to calculate the public key, a point on the curve, by multiplying the base point P with a large random number (your private key).
But if an adversary knows the base point P and your public key, he cannot divide them and say how many times P was added to itself to get your public key.
At this point, your public key is pretty large, 512 bit, and it is easy to compress it to half the size. The elliptic curve is symmetric about the x-axis. There are only two possible y-values for every x-value that only differ in their sign (being positive or negative).
If you leave out the y-coordinate and add the information of the point having a positive or negative value for y, the public key becomes half the size but carries the same information.
Address
Lastly, to get your address, your public key is hashed. First, using the SHA-256 hash function and a second time using RIPEMD 160. After adding a byte to state if this address will go to the main or test net and calculating a checksum, there is a final step before you get your address.
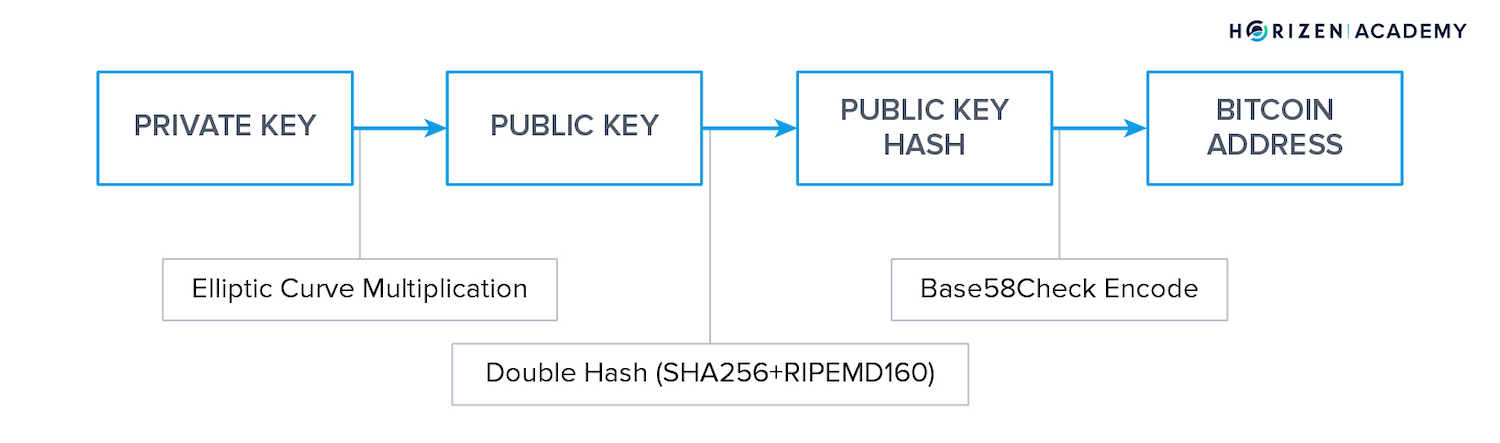
When we look at how a computer is working at the hardware level it is zeros and ones. Data is always stored in a binary format no matter what type of data you’re looking at, whether images, sound files, and even your Bitcoin address.
There are different ways to convert a string of bits into data that humans can digest. Humans do best with a string of numbers or alphanumeric characters.
Base58Check is a way to convert bits into alphanumeric characters, but it excludes the four characters 0, O, I, and l. Base58Check removes these characters from your address to reduce errors when copying addresses manually and proofreading them.
Cobalt is a secure and easy-to-use web extension wallet for the Horizen cross-chain ecosystem. Trustworthy, reliable and built to easily manage your assets.
You can generate as many addresses as you like from a single private key, and wallets do this for you automatically. It is a feature to enhance your privacy, as it makes it harder for a third party to link all your payments together.
Digital Signature
You might hear that your keys are used to encrypt and decrypt messages.
This is true, but it is not why we use public-key cryptography on the blockchain. The information contained within transactions is not encrypted in any way. It is available to anyone on the blockchain, which makes the system so transparent.
What your private key is actually necessary for on the blockchain is signing transactions. You can only spend funds you received in a transaction if you provide a digital signature that proves your knowledge of the private key corresponding to the address used to receive the funds.
Summary - Public-Key Cryptography
When you set up a wallet, the software will first generate a large random number that is your private key.
The base point P on the elliptic curve is multiplied with your private key to get your public key, another point on the curve.
Your public key is then hashed and the characters I, l, 0 and O are removed to improve readability. To spend your money you need to provide a digital signature that proves your knowledge of the private key that belongs to your address.